Produtos Notáveis

Ao lidarmos com operações algébricas, perceberemos que alguns polinômios aparecem frequentemente e, ainda, exibem certa regularidade. Esses são os produtos notáveis.

 Aqui estudaremos 

• O quadrado da soma de dois termos, 
• O quadrado da diferença de dois termos, 
• O produto da soma pela diferença de dois temos, 
• O cubo da soma de dois termos e, por fim, o cubo da diferença de dois termos. 

Vamos à explicação de cada um deles:

1.    O quadrado da soma de dois termos

Verifiquem a representação e utilização da propriedade da potenciação em seu desenvolvimento.

(a + b)² = (a + b) . (a + b)

Onde a é o primeiro termo e b é o segundo.

Ao desenvolvermos esse produto, utilizando a propriedade distributiva da multiplicação, teremos:

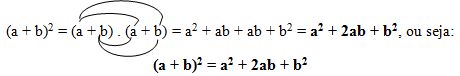
O quadrado da soma de dois termos é igual ao quadrado do primeiro termo, mais duas vezes o produto do primeiro termo pelo segundo, mais o quadrado do segundo termo.

Exemplos:

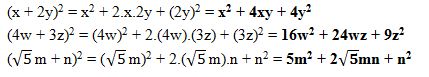
2.    O quadrado da diferença de dois termos

Seguindo o critério do item anterior, temos:

(a - b)² = (a - b) . (a - b)

Onde a é o primeiro termo e b é o segundo.

 Ao desenvolvermos esse produto, utilizando a propriedade distributiva da multiplicação, teremos:

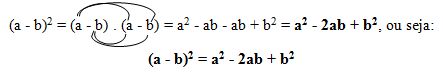
O quadrado da diferença de dois termos é igual ao quadrado do primeiro termo, menos duas vezes o produto do primeiro termo pelo segundo, mais o quadrado do segundo termo.

Exemplos:

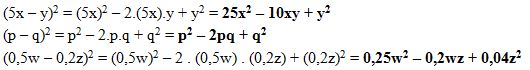
3. O produto da soma pela diferença de dois termos

Se tivermos o produto da soma pela diferença de dois termos, poderemos transformá-lo numa diferença de quadrados.

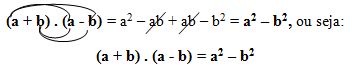
O produto da soma pela diferença de dois termos é igual ao quadrado do primeiro termo, menos o quadrado do segundo termo.

Exemplos:

• (4c + 3d).(4c – 3d) = (4c)² – (3d)² = 16c² – 9d²
• (x/2 + y).(x/2 – y) = (x/2)² – y² = x²/4 – y²
• (m + n).(m – n) = m² – n²

4. O cubo da soma de dois termos

Consideremos o caso a seguir:

(a + b)³ = (a + b).(a + b)² → potência de mesma base.

(a + b).(a² + 2ab + b²) → (a + b)²

Aplicando a propriedade distributiva como nos casos anteriores, teremos:

(a + b)³ = a³ + 3a²b + 3ab² + b³

O cubo da soma de dois termos é igual ao cubo do primeiro termo, mais três vezes o produto do quadrado do primeiro termo pelo segundo, mais três vezes o produto do primeiro termo pelo quadrado do segundo, mais o cubo do segundo termo.

Exemplos:

• (2x + 2y)³ = (2x)³ + 3.(2x)².(2y) + 3.(2x).(2y)² + (2y)³ = 8x³ + 24x²y + 24xy² + 8y³
• (w + 3z)³ = w³ + 3.(w²).(3z) + 3.w.(3z)² + (3z)³ = w³ + 9w²z + 27wz² + 27z³
• (m + n)³ = m³ + 3m²n + 3mn² + n³

5. O cubo da diferença de dois termos

Acompanhem o caso seguinte:

(a – b)³ = (a - b).(a – b)² → potência de mesma base.

 (a – b).(a² – 2ab + b²) → (a - b)²

Aplicando a propriedade distributiva como nos casos anteriores, teremos:

(a – b)³ = a³ – 3a²b + 3ab² – b³

O cubo da diferença de dois termos é igual ao cubo do primeiro termo, menos três vezes o produto do quadrado do primeiro termo pelo segundo, mais três vezes o produto do primeiro termo pelo quadrado do segundo, menos o cubo do segundo termo.

Exemplos:

• (2 – y)³ = 2³ – 3.(2²).y + 3.2.y² – y³ = 8 – 12y + 6y² – y³ ou y³– 6y²  +  12y – 8
• (2w – z)³ = (2w)³ – 3.(2w)².z + 3.(2w).z² – z³ = 8w³ – 12w²z + 6wz² – z³
• (c – d)³ = c³ – 3c²d + 3cd² – d³

Frações Algébricas

Fração algébrica, em álgebra elementar, é uma fração em que contém incógnita no denominador. Em, a incógnita no denominador, faz com que a fração seja algébrica. Essa terminologia de fração, indica o quociente de polinômios. Nela, uma ou mais variáveis aparecem no denominador.

O cálculo de frações algébricas utiliza o mesmo processo do cálculo das frações numéricas, admitindo-se sempre que o denominador não seja nulo, ou seja, diferente de zero.

Simplificação de frações algébricas:

   

 A simplificação de frações é feita dividindo o numerador e o denominador pelo mesmo número, isto seria o mesmo que eliminar todos os fatores comuns, obtendo uma fração mais simples e equivalente. Observe os exemplos: 

Com base nesse mesmo procedimento, simplificamos frações algébricas que apresentam fatores em comum. Veja exemplos: 

Cálculo do m.m.c de polinômios

O mínimo múltiplo comum de números naturais ou de polinômios será encontrado através da comparação dos fatores de cada fatoração, ou seja, o mmc de um número natural ou de um polinômio é a multiplicação dos fatores sem repetir os comuns, levando em consideração os de maior expoente. 


Exemplo: Ao calcularmos o mmc de 8 e 18 é preciso fatorar o 8 e o 18 em fatores primos, ficando da seguinte forma: 

8 = 2 * 2 * 2 = 2³. Sendo 2³ o único fator dessa fatoração. 

18 = 2 * 3 * 3 = 2 * 3². Sendo 2 e 32 os fatores dessa fatoração. 

Os fatores comum são 2³ e 2, dessa forma consideramos o 2³. Assim, o mmc de 8 e 18 será igual a 2³ * 3² = 72. 

Exemplo: mmc de 9xy e 12 xy². Fatoramos separadamente cada monômio. 

9xy = 3² * x * y. Sendo 3² e x e y os fatores dessa fatoração. 

12xy² = 2² * 3 * x * y². Sendo 2² e 3 e x e y² os fatores dessa fatoração. 

Os fatores comum são 3² e 3, x e x, y e y², seguindo a regra iremos considerar 3², x, y². 
Dessa forma, podemos dizer que o mmc de 9xy e 12xy² é igual a 3² * 2² * x * y² = 36xy². 

Exemplo: mmc de x² + 1 e x² – 2x + 1. Fatoramos separadamente cada polinômio. 

x² – 1 = (x + 1) * (x – 1) 

x² – 2x + 1 = (x – 1)² 

Os fatores comum são (x – 1)² e (x – 1), seguindo a regra iremos considerar (x – 1)². Dessa forma, podemos dizer que o mmc de x² + 1 e x² – 2x + 1 é igual a (x + 1) * (x –1)². 

A utilização do MMC de polinômios está diretamente ligada às resoluções de equações fracionárias algébricas, pois esse tipo de equação traz em seu denominador monômios, binômios, trinômios ou polinômios. Dessa forma, se uma equação fracionária algébrica apresentar denominadores diferentes, utilizaremos o MMC de polinômios. Observe uma aplicação do mmc de polinômios na resolução de uma equação. 

Exemplo 1

   

Adição e subtração com frações algébrica:

   

 Quando as frações possuem o mesmo denominador, basta somar ou subtrair os numeradores.

Ex:   

x + y    +   2x + y    =  3x + 2y

     z              z               z

    Quando as frações possuem denominadores diferentes, basta reduzi-las ao mesmo denominador e em seguida, somar ou subtrair os numeradores.

Ex:   

a + b  +  2a + 3b   =    a + b  +  2(2a + 3b)    =    a + b    +   4a + 6b =  5a + 7b

    4              2              4               4                   4                4              4

Multiplicação e divisão de frações algébricas

    

Para multiplicar ou dividir frações algébricas, usamos o mesmo processo das frações numéricas. Fatorando os termos da fração e simplificar os fatores comuns.

Exemplos:

Fatoração de Expressões Algébricas

Fatoração de um número

Fatorar um número significa representa-lo pela multiplicação de dois ou mais fatores que são divisores do número em questão.

É possível representar um número como uma multiplicação de dois ou mais fatores. Observe, por exemplo, estas formas de representar o número 60:

60 = 6 x 10          60 = 4 x 3 x 5         60 = 2² x 3 x 5

Assim, efetua-se a fatoração, ou decomposição,do número 60. Observe que, em cada caso, os fatores são divisores do número fatorado. No terceiro caso, tem-se o número 60 representado pela multiplicação de fatores primos( lembrando: número primo é aquele que tem apenas dois divisores distintos, o 1 e ele mesmo).

Exemplos:

• O produto 3 x 15 é uma forma fatorada do número 45.
• O produto 2 x 3 x 7 é uma forma fatorada do número 42.
• O produto 1 x 13 é a forma fatorada do número 13.
  
  
  
  
  Fator comum em evidência  
  
  
  Nesse modelo de fatoração temos que determinar o elemento comum aos termos que formam o polinômio. Observe:
  
  
  No polinômio x² + 2x, temos que a variável x é comum aos dois termos. Ela será o termo em evidência, a qual dividirá todos os termos do polinômio original.
  
  
  x² + 2x → x * (x + 2)
  x² : x = x
  2x : x = 2
  
  
  Veja mais exemplos de fatoração por evidência:
  
  
  4x³ – 2x² → 2x² * (2x – 1)
  4x³ : 2x² = 2x
  2x : 2x = 1
  
  
  16x² + 8 → 8 * (2x² + 1)
  16x² : 8 = 2x²
  8 : 8 = 1
  
  
  
  
  Agrupamento
  
  

A expressão ax + bx + ay + by representa a soma de quatro parcelas e não há nenhum fator comum para as quatro.

No entanto, se agruparmos ax + bx ou ay + by podemos colocar em evidência tanto o x quanto o y. Assim, a expressão transforma-se em duas parcelas, e em ambas aparecerá um novo fator comum a + b, também podendo ser colocado em evidencia. 

Observe:

ax + bx + ay + by = x . (a + b) + y . (a + b) = (a + b) . (x + y). 

Exemplos 

ax + ay + 2x + 2y = a (x +y) +2 . (x + y) = (x + y) . (a + 2).

mm + 3m + 4n + 12 = m . (n + 3) + 4 . (n + 3) = (n + 3) . (m + 4).

a2 – ab – 2a + 2b = a . (a – b) – 2 . (a – b) = (a – b) . (a – 2).

a2 + ab + a + b = a . (a + b) + 1 . (a + b) = (a + b) . (a + 1).

mn – m – n + 1 = m . (n – 1) – 1 . (n – 1) = (n – 1) . (m – 1).

Diferença de dois quadrados

Para compreendermos melhor como e quando utilizarmos é necessário que saibamos que diferença na matemática é o mesmo que subtração e que quadrado é elevar um número, letra ou termos ao quadrado. 

A fatoração pela diferença de dois quadrados só poderá ser usada quando: 

- Tivermos uma expressão algébrica com dois monômios (sejam binômios). 
- Os dois monômios sejam quadrados. 
- A operação entre eles for de subtração. 

Veja alguns exemplos de expressões algébricas que seguem esse modelo: 


• a² - 1, a expressão algébrica tem apenas dois monômios, os dois estão ao quadrado e entre eles há uma operação de subtração. 
• 1 – a² 
   3 
• 4x² – y² 

^{Trinômios quadrados perfeitos}

 Para fatorar uma expressão algébrica utilizando o trinômio quadrado perfeito a expressão deverá ser um trinômio e formar um quadrado perfeito.

Então, para compreender melhor esse tipo de fatoração vamos recapitular o que é um trinômio e quando um trinômio pode ser um quadrado perfeito.

Trinômio 
Para que uma expressão algébrica seja considerada um trinômio, ela deverá conter exatamente 3 monômios. Veja alguns exemplos de trinômios:

x³ + 2x² + 2x

- 2x⁵ + 5y – 5

ac + c – b

É importante ressaltar que nem todos os trinômios são quadrados perfeitos. É preciso verificar se um trinômio pode ser escrito na forma de um quadrado perfeito.

Quadrado perfeito

Veja a demonstração do que é um quadrado perfeito:

Um número é um exemplo de quadrado perfeito, basta que esse número seja o resultado de outro número elevado ao quadrado, por exemplo: 36 é um quadrado perfeito, pois 6² = 36.
Agora, para aplicar isso em uma expressão algébrica, observe o quadrado (todos os lados iguais) abaixo com lados x + y. O valor desse lado é uma expressão algébrica.



Para calcularmos a área desse quadrado podemos seguir duas formas diferentes:

1º forma: A fórmula para o cálculo da área do quadrado é A = Lado², então como o lado nesse quadrado é x + y, basta elevá-lo ao quadrado.

A1 = (x + y) . (x + y) que é o mesmo que A1 = (x + y)², então podemos dizer que:

O resultado dessa área A1 = (x + y)² é um quadrado perfeito.

2º forma: Esse quadrado foi dividido em quatro retângulos, onde cada um tem a sua própria área, então a soma de todas essas áreas é a área total do quadrado maior, ficando assim:

A2 = x² + xy + xy + y², como xy e xy são semelhantes podemos somá-los

A2 = x² +2xy + y²

O resultado da área A2 = x² +2xy + y² é um trinômio.


As duas áreas encontradas representam a área do mesmo quadrado, então:

  A1       =         A2
(x + y)² = x² +2xy + y2

Então, o trinômio x2 +2xy + y2 tem como quadrado perfeito (x + y)2.

Quando tivermos uma expressão algébrica e ela for um trinômio do quadrado perfeito, a sua forma fatorada é representada em forma de quadrado perfeito, veja:

O trinômio x² +2xy + y² fatorado fica (x + y)².

Como já foi dito, nem todos os trinômios são quadrados perfeitos, por isso é preciso que saibamos identificar se um trinômio é quadrado perfeito ou não. Veja como é feita essa identificação:

Quando um trinômio é quadrado perfeito

O quadrado perfeito (x + y)² é composto por dois fatores (x e y). A resolução dele é um trinômio x²+2xy + y². O primeiro monômio é o quadrado do primeiro termo; o segundo monômio é duas vezes o primeiro termo vezes o segundo; e o terceiro monômio é o quadrado do segundo termo.

Esse trinômio do quadrado perfeito é considerado uma forma geral seguida para qualquer quadrado perfeito.

Portanto, para que um trinômio seja quadrado perfeito ele tem que seguir esse modelo. Fazendo um resumo podemos dizer que:

Para que um trinômio seja quadrado perfeito ele deve ter algumas características:

• Dois termos (monômios) do trinômio devem ser quadrados.
• Um termo (monômio) do trinômio deve ser o dobro das raízes quadradas dos dois outros termos.

Veja alguns exemplos:

Veja se o trinômio 9a² – 12ab + 4b² é um quadrado perfeito. Para isso, siga as regras que foram citadas.



Dois membros do trinômio 9a² – 12ab + 4b² têm raízes quadradas e o dobro delas é o termo do meio, então o trinômio é quadrado perfeito.

Então, a forma fatorada do trinômio 9a² – 12ab + 4b² é (3a – 2b)², pois é a soma das raízes ao quadrado.

Exemplo:

Dado o trinômio 4x² – 8xy + y², devemos tirar as raízes dos termos 4x² e y², as raízes serão respectivamente 2x e y. O dobro dessas raízes deve ser 2 . 2x . y = 4xy, que é diferente do termo 8xy, então esse trinômio não poderá ser fatorado utilizando o quadrado perfeito.

Soma de dois cubos

A Soma de dois cubos é o caso de fatoração de expressões algébricas, para que entenda como e quando devemos utilizá-lo observe a sua demonstração abaixo: 

Dado dois números quaisquer x e y, se somarmos os dois obteremos x + y, se montarmos uma expressão algébrica com os dois números teremos x² - xy + y², agora devemos multiplicar as duas expressões encontradas. 

(x + y) (x² - xy + y²) utilize a propriedade distributiva 

x³ - x²y + xy² + x²y –xy² + y³ unir os termos semelhantes 

x³ + y³ é uma expressão algébrica de dois termos onde os dois estão elevados ao cubo e somados. 

Assim, podemos concluir que x³ + y³ é uma forma geral da soma de dois cubos onde 
x e y poderão assumir qualquer valor real. 

A forma fatorada de x3 + y3 será (x + y) (x² - xy + y²). 

Veja alguns exemplos: 

Exemplo1: 
a³ + 1000 é a soma de dois cubos. 

Podemos escrever essa expressão da seguinte forma: 

a³ + 103, assim: x = a e y = 10 
Agora basta usarmos a forma geral e fazermos as substituições. 

(x + y) (x² - xy + y²) 
(a + 10) (a² – a10 + 10²) 
(a + 10) (a² – 10a + 100) 

Portanto, a fatoração de a³ + 10³ será (a + 10) (a² – 10a + 100). 

Exemplo 2: 
27x³ + 1 é a soma de dois cubos. 
Podemos escrever essa expressão da seguinte forma: 

(3x)³ + 1 assim: x = 3x e y = 1 
Agora basta usarmos a forma gral e fazermos as substituições. 

(x + y) (x² - xy + y²) 

(3x + 1) ((3x)² – 3x .1 + 1²) 

(3x – 1) (9x² – 3x + 1) 

Exemplo 3: 
8x³ + y³ é a soma de dois cubos. 
Podemos escrever essa expressão da seguinte forma: 

(2x)³ + y³ assim: x = 2x e y = y 
Agora basta usarmos a forma gral e fazermos as substituições. 

(x + y) (x² - xy + y²) 

(2x + y) ((2x)² – 2xy + y²) 

(2x + y) (4x² – 2xy + y²)

Diferença de dois cubos

A diferença de dois cubos é caso de fatoração de expressões algébricas, o seu raciocínio é o mesmo da soma de dois cubos, raciocínio esse que esclarece como e quando devemos utilizá-lo, observe a demonstração abaixo: 

Dado dois números quaisquer x e y. Se subtrairmos ficará: x – y, se montarmos uma expressão algébrica com os dois números obteremos: x2 + xy + y2, assim, devemos multiplicar as duas expressões encontradas. 

(x - y) (x2 + xy + y2) é necessário utilizar a propriedade distributiva; 

x3 + x2y + xy2 - x2y –xy2 - y3 unir os termos semelhantes; 

x3 - y3 é uma expressão algébrica de dois termos, os dois estão elevados ao cubo e subtraídos. 

Assim, podemos concluir que x3 - y3 é uma forma geral da soma de dois cubos onde 

x e y podem assumir qualquer valor real. 

A forma fatorada de x3 - y3 será (x - y) (x2 + xy + y2). 

Veja alguns exemplos: 

Exemplo1 

Se tivermos que fatorar a seguinte expressão algébrica 8x3 – 27, devemos observar que ela tem dois termos. Lembrando dos casos de fatoração, o único caso que fatora dois termos é a diferença de dois quadrados, soma de dois cubos e a diferença de dois cubos. 

No exemplo acima os dois termos estão ao cubo e entre eles há uma subtração, então devemos utilizar o 7º caso de fatoração (diferença de dois cubos), para fatorarmos deveremos escrever a expressão algébrica 8x3 – 27 da seguinte forma: 

(x - y) (x2 + xy + y2). Ao tirar as raízes cúbicas dos dois termos, temos: 8x3 – 27 

A raiz cúbica de 8x3 é 2x e a raiz cúbica de 27 é 3. Agora, basta substituir valores, no lugar de x colocaremos 2x e no lugar de y colocaremos 3 na forma fatorada 

(x - y) (x2 + xy + y2) , ficando assim: 

(2x – 3) ((2x)2 + 2x . 3 + 32) 

(2x – 3) (4x2 + 6x + 9) 

Então, (2x – 3) (4x2 + 6x + 9) é a forma fatorada da expressão algébrica 8x3 – 27. 

Exemplo 2 

Para resolvemos a fatoração utilizando a diferença de dois cubos devemos seguir os mesmos passos do exemplo anterior. Fatorando a expressão algébrica r3 – 64 temos: As raízes cúbicas de r3 é r e de 64 é 4, substituindo teremos no lugar de x o r e no lugar de y o 4. 

(r – 4) (r2 + 4r + 16) é a forma fatorada de r3 – 64.